Say you have a collection of elements, and you want to group them into a number of sets (that are each disjoint). One example could be grouping nodes within a graph that are connected by a path of edges.

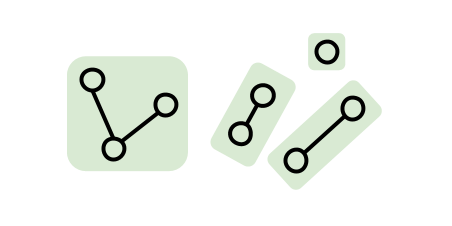
There are a number of different data structures you could use to do this, but one which I find particularly elegant is a disjoint set.

• Yes, the plurality is weird here. I tend to just go with "disjoint set" and not think too much about it.
• Yes, I do have a favourite data structure. So should you!

Basic Operations

Our data structure supports three operations:

• insert(element): Inserts element, putting it in its own set. You may see this called "makeSet" elsewhere.
• union(lhs, rhs): Union the two sets containing lhs and rhs (which should have been previously inserted).
• sameSet(lhs, rhs) -> Bool: Determine whether lhs and rhs (which should have been previously inserted) are in the same set. You may see other implementations have a "findSet" method instead, that returns a "representative object" for the set containing an element (which can be compared with another to see if two elements are in the same set). I prefer going with sameSet directly.

Each set will be represented internally as its own tree. With this representation, the three operations are pretty simple to implement.

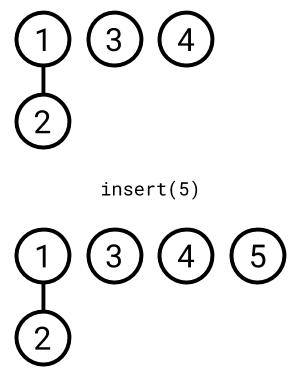
insert(element)

• Create a new tree for element.

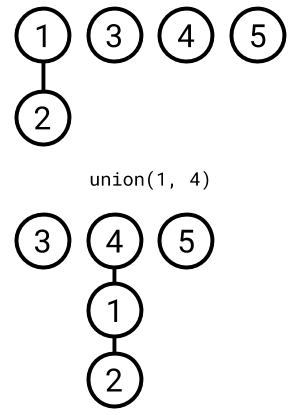
union(lhs, rhs)

• Take the root for the tree containing lhs.
• Take the root for the tree containing rhs.
• If different, move one root to be a child of the other.

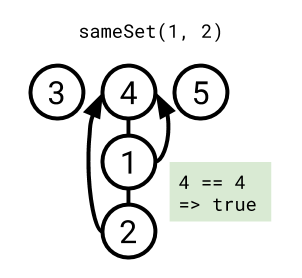
sameSet(lhs, rhs) -> Bool

• Take the root for the tree containing lhs.
• Take the root for the tree containing rhs.
• Return true if they're the same, otherwise false.

Improvements

The above is all we need to get something working, but there are two heuristics that we can use to improve performance.

• Union by rank: When performing union, if one tree is shorter than the other, then move that one. This makes sense if you think about it; we want to try and reduce the length of the path we may need to travel when finding the root of a tree, so we want our trees to be as short as possible.

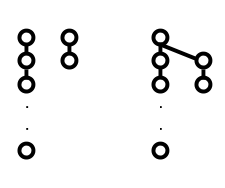
The right tree is much shorter than the left, so root it under the left tree on union.

• Path compression: When travelling from a node up to the root of its tree (during a union, or sameSet operation), move the nodes in the path to point at the root. This way, the next time you need to travel the path, there's only be a single hop to go for each node. The rationale here is similar to that for union by rank: we want our trees to be as short as possible.

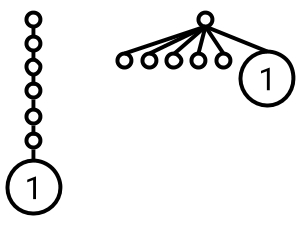
After performing an operation such as sameSet(4, other), all nodes on the path from 4 to the root are moved directly under the root. This makes the paths shorter next time around.

Time Complexity

(Here comes the punchline.)

With those two heuristics in place, it can be shown (using a proof that I admittedly don't understand) that any sequence of m insert, union and sameSet operations can be performed in O(mα(n)) time (where n is the number of inserted elements). α(n) is the inverse of the Ackermann function, which grows so slowly that α(<number of atoms in the universe>) < 5, so this term is effectively a constant.

Therefore, the amortized complexity of each operation is O(1); each operation is effectively performed in constant time.

How cool is that? I love how such a simple data structure with a few optimizations results in a time complexity based on a function so weird as the Ackermann function.

Example Implementation

An example implementation in Swift is below (or in a Gist, if you prefer). I've tried to thoroughly document the implementation but feel free to reach out if something doesn't make sense.

/// Maintains a number of sets, each containing a number of
/// `Element`s.
///
/// Supports union-ing two sets (using an `Element` contained in
/// each set), as well as determining whether two `Element`s are
/// contained within the same set.
///
/// Note that this is a reference type, rather than a struct
/// with value semantics. This is due to the complexity of
/// copying  the `Node`s on write, which whilst possible,
/// detracts from  the actual behaviour of the type in this
/// example.
public final class DisjointSet<Element: Hashable> {

  // MARK: - Types

  /// `Error` thrown when an operation expects than an element
  /// has already been inserted with `insert(_:)`.
  public struct MissingElementError: Error {}

  /// A single node in a set.
  ///
  /// Note that this is a reference type, since each `Node` will
  /// be stored in the `nodes` dictionary (to lookup `Node`s by
  /// an `Element`), and will be referred to by other `Node`s in
  /// its set.
  private final class Node {
    /// The parent `Node`.
    ///
    /// Will be `nil` if this `Node` is the  root node of a set.
    var parent: Node?

    /// An upper-bound on the number of child nodes of this
    /// `Node`.
    var rank: Int = 0
  }

  // MARK: - Properties

  /// A mapping of `Element`s to `Node`s, containing a `Node`
  /// for each `Element` that has been inserted by `insert(_:)`.
  private var nodes: [Element: Node] = [:]

  // MARK: - Initializers

  /// Initializes a `DisjointSet` that initially contains 0
  /// elements.
  public init() {}

  // MARK: - Public

  /// Inserts the specified `element`.
  ///
  /// - Returns: `true` if `element` was inserted, or `false`
  ///   otherwise (e.g. if `element` has already been inserted).
  @discardableResult public func insert(
    _ element: Element
  ) -> Bool {
    guard nodes[element] == nil else {
      // Element already inserted.
      return false
    }
    nodes[element] = Node()
    return true
  }

  /// Unions the two sets containing `lhs` and `rhs`.
  ///
  /// - Parameters:
  ///   - lhs: An element contained in the first set.
  ///   - rhs: An element contained in the second set.
  /// - Throws: A `MissingElementError` if either `lhs` or `rhs`
  ///   has not previously been inserted.
  public func union(_ lhs: Element, _ rhs: Element) throws {
    guard 
      let lhsNode = nodes[lhs],
      let rhsNode = nodes[rhs]
    else {
      throw MissingElementError()
    }
    let lhsRoot = findRoot(node: lhsNode)
    let rhsRoot = findRoot(node: rhsNode)
    guard lhsRoot !== rhsRoot else {
      // `lhs` and `rhs` are already in the same set.
      return
    }

    // Union by rank heuristic.
    if lhsRoot.rank > rhsRoot.rank {
      // Note: `lhsRoot.rank` is intentionally not incremented
      // here. `lhsRoot.rank` is still valid, since it is just
      // an upper bound (and the new child, `rhsRoot`, has a 
      // lower rank).
      rhsRoot.parent = lhsRoot
    } else if lhsRoot.rank < rhsRoot.rank {
      // Note: `rhsRoot.rank` is intentionally not incremented
      // here (same reasoning as above).
      lhsRoot.parent = rhsRoot
    } else {
      // `lhsRoot.rank == rhsRoot.rank`. Use `rhsRoot` as the
      // new root arbitrarily.
      lhsRoot.parent = rhsRoot
      // `rhsRoot.rank` needs to be updated here to ensure that
      // the upper bound is still valid.
      rhsRoot.rank += 1
    }
  }

  /// Returns `true` if `lhs` and `rhs` are members of the same
  /// set.
  ///
  /// - Parameters:
  ///   - lhs: The first `Element` to check for co-membership.
  ///   - rhs: The second `Element` to check for co-membership.
  /// - Throws: `true` if `lhs` and `rhs` are contained in the
  ///   same set (as a result of a `union(_:_:)` operation.
  /// - Returns: A `MissingElementError` if either `lhs` or
  ///   `rhs` has not previously been inserted.
  public func sameSet(
    _ lhs: Element, 
    _ rhs: Element
  ) throws -> Bool {
    guard 
      let lhsNode = nodes[lhs], 
      let rhsNode = nodes[rhs] 
    else {
      throw MissingElementError()
    }
    /// Use `===` to check for instance equality, rather than
    /// value equality.
    return findRoot(node: lhsNode) === findRoot(node: rhsNode)
  }

  // MARK: - Private

  /// Returns the root `Node` pointed to be `node`, or `node`
  /// itself if it is a root node.
  private func findRoot(node: Node) -> Node {
    if let parent = node.parent {
      // Path compression heuristic.
      node.parent = findRoot(node: parent)
    }
    // If `node.parent` is `nil`, `node` is a root node.
    // Therefore, return it instead.
    return node.parent ?? node
  }

}